Как рассчитать объем комнаты в м3: Ничего не найдено для d0 ba d0 b0 d0 ba d0 bf d0 be d1 81 d1 87 d0 b8 d1 82 d0 b0 d1 82 d1 8c d0 be d0 b1 d1 8a d0 b5 d0 bc d0 bf d0 be d0 bc d0 b5 d1 89 d0 b5 d0 bd d0 b8 d1 8f d0 b2 d0 bc3

Как найти объем помещения. Как рассчитать, посчитать объем помещения

 

Как рассчитать, посчитать объем помещения.

Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.

1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.

2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.

3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.

4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.

5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.

Формула объема помещения

Формула

 

Пример расчета объема помещения по формуле

Калькулятор площади стены или пола

Вставьте размеры помещения и получите результат.

Как посчитать кубатуру помещения сложной формы: пошаговая инструкция

Под кубатурой помещения обычно подразумевается его объем, выраженный в кубических метрах. Если известны основные параметры помещения (длина, ширина и высота), то вычислить его кубатуру очень просто.

Однако, если строение имеет сложную форму, то посчитать его объем бывает довольно-таки затруднительно.

Как это сделать правильно. Для это нужно заглянуть на страницы он-лайн журнала ProfiDom.com.ua и прочитать нижеследующую пошаговую инструкцию

Для вычисления объемы помещения нам понадобится только калькулятор.

Шаг 1. Чтобы вычислить кубатуру помещения перемножьте его длину, ширину и высоту. То есть воспользуйтесь формулой:

К = Д х Ш х В, где:

К – кубатура помещения (объем, выраженный в кубических метрах),

Д, Ш и В – длина, ширина и высота помещения, выраженные в метрах, соответственно.

Например, если длина помещения составляет 11 метров, ширина – 5 метров, а высота – 2 метра, то его кубатура будет 11 х 5 х 2 = 110 кубометров.

Шаг 2. Если одна или несколько характеристик помещения неизвестны, то измерьте их, воспользовавшись строительной рулеткой или электронным дальномером. При использовании электронного дальномера следите, чтобы он был направлен строго перпендикулярно той стене, расстояние до которой измеряется. Чтобы повысить точность вычислений, высоту и ширину измерьте дважды – у противоположных стен, а затем найдите среднее арифметическое (сложите и разделите на 2).

Шаг 3. Пусть, например, измерения длины помещения показали 10,01 м и 10,03 м, измерения ширины – 5,25 м и 5,26 м, а измерение высоты – 2,50 м. В таком случае, кубатура помещения будет равняться:

(10,01+10,03)/2 х (5,25+5,26)/2 х 2,5 = 131,638

(в большинстве случаев, трех знаков после запятой вполне достаточно).

Шаг 4. Если известка площадь помещения, то для вычисления кубатуры просто умножьте эту площадь на высоту. Т.е., используйте формулу:

К = П х В, где 

П – площадь помещения, заданная в квадратных метрах (м²).

Так, например, если площадь помещения равняется 100 квадратных метров, а его высота – 3 метра, то его объем будет: 

100х3=300 (метров кубических).

Шаг 5. Если помещение имеет сложную форму, то для определения его площади воспользуйтесь соответствующими геометрическими формулами или разделите помещение на более простые участки. 

Так, например, арена цирка всегда имеет форму круга радиусом 13 метров. Следовательно, ее площадь будет равна πR²=3,14 х 169 = 531 (метр квадратный).

Если же, например, помещение состоит из трех комнат площадью 30, 20 и 50 м², то общая площадь помещения будет равняться 100 м².

Калькулятор для расчета объёма груза. Как посчитать объём (м3)

Расчет
объема

Количество коробок

Рассчитать объём

Результат:

Объем одной
коробки(м³):

Общий
объем(м³):

Используйте полученный

результат для

оформления заявки

Количество труб

Рассчитать объём

Результат:

Объем одной трубы(м³):

Общий
объем(м³):

Используйте полученный

результат для

оформления заявки

У вас возник вопрос о доставке, а так же возникла необходимость знать, как вычислить объем груза, нужна наша помощь? Как вычислить объем груза мы знаем, на этой странице вы видите калькулятор, который точно выполнит расчеты.

А вообще, для какой цели рассчитывается объем?

Объем рассчитать необходимо для того, чтобы избежать недоразумений при погрузке груженых коробок в транспортное средство. Объем рассчитать при помощи современных технологий сегодня несложно, достаточно вашего нахождения тут.

Какие критерии мы используем для подсчета объема груза?

Во-первых, все знают – в процессе доставки важна каждая деталь, и немаловажно без ошибок посчитать объем груза в целом. Посчитать объем груза как уже говорилось поможет наш калькулятор объемов, он сделает это быстро и надежно!

Второе – калькулятор объемов, о его начини на нашем сайте, уже сказано выше, как видите, мы заботимся о наших клиентах. Калькулятор объемов, вот что может максимально облегчить работу с расчетами, и напрочь убить ваши сомнения.

Что мы вам даём?

Условия для умения объем груза рассчитать самостоятельно, т. е. это и формулы, пояснения к ним, и даже калькулятор. Объем груза рассчитать при таких возможностях можно за считанные минуты, главное не допустить никаких ошибок.

Что же еще необходимо?

Например…

Вы предприниматель, который занимается перевозками из Китая, и Вам постоянно необходим калькулятор расчета объема. Калькулятор расчета объемов вы быстро найдёте на страницах нашего сайта, и выполните свои расчеты сейчас же.

И все же.

В наше время предпринимательство держится на Китайском производстве товаров, а от куда возникла потребность рассчитать объем? Рассчитать объем необходимо для того что бы узнать общий объём груза, и далее выбрать вид транспорта.

Чем же является расчет объемов в доставке? И какую роль он играет?

Расчёт объема — это насколько, вы уже поняли очень важный этап в доставке, и доверять его надо в надёжные руки профессионалов. Расчёт объема груза надо делать тщательно, учитывая все размеры, и переведя их в метры кубические.

Но к сожалению, не все справляются с этими расчетами.

Еще в школьные времена мы изучали то как посчитать объем груза в м3, но к сожалению, всего этого не запомнишь. Как посчитать объем груза в м3 – бывают случаи когда этот вопрос встаёт на первое место, например во время доставки.

Для этого данная страница и существует!

Мы готовы объяснить, как посчитать объем м3, ведь это можно сделать самостоятельно или что бы проверить наши расчеты. Как посчитать объем м3, для этого необходимо перевести размеры в метры, затем перемножить, формула: Д*Ш*В.

Ведь эта страница для того и предназначена, чтобы помогать Вам в расчёте доставки.

Что бы выполнить расчет объема коробки, не надо стараться это делать самостоятельно, просто надо заполнить пустые поля. Расчет объема коробки автоматически выполнится нашим калькулятором, если вы сомневаетесь, проверьте сами.

Для этого мы и напомнили Вам формулу объемов.

Зачем вообще надо знать то, как рассчитать кубатуру?

Расчет объема груза в кубометрах необходим Вам для того, чтобы подать правильную заявку для его перевозки. Расчет объема груза в кубометрах, т. е. знание самого объема поможет определиться с тем какой вид доставки Вам подойдет.

А теперь перейдем к основному, поговорим о том, как совершать расчеты и для чего они необходимы.

Для начала разберемся…

А все ли помнят, что такое объем как посчитать его, формулу расчёта, конечно же большинство людей забыло, как и что это. Объем как посчитать его, пишется и объясняется в формулах, приведенных в статье, остается указать размеры.

Рассчитать объем груза не всегда просто, как кажется, всё это из-за того что, коробки могут быть разнообразной формы. Рассчитать объем груза прямоугольной коробки, пустяк, а вот остальных тяжеловато, необходимо знать формулы.

Для начала определим форму, для этого сначала узнаем, какие они существуют.

Какую форму может иметь коробка:

• Куб;
• Прямоугольника;
• Цилиндра;
• Усеченной пирамиды (очень редко).

Затем следуют измерения

Перед тем, как вычислить объем коробки измерим её, но запомните, чем точнее сделаны измерения, тем легче Вам. «Как вычислить объем коробки?» — что делать дальше: определить, какой она формы (куба или прямоугольника), размеры.

Что нам дает знание объёма?

Знание объёма коробки не позволит допустить недоразумений при погрузке товаров в любой вид транспорта, который может быть. От объёма коробки практически не чего не зависит, скорее наоборот все зависит от размеров самого товара.

А почему? Тут всё очевидно, прежде чем приобрести коробку, надо узнать размер груза, который Вы собираетесь перевозить через границу.

Ну вот Вы знаете размеры груза, теперь остаётся посчитать его объем (что бы приобрести коробу).

Итак, для того чтобы узнать, как рассчитать объем груза в м3 формула потребуется в первую же очередь. Как рассчитать объём груза в м3 формула поможет без сомнений в этом вопросе, вот так она выглядит V=a*b*h, всё очень просто.

Тем более она уже вам известна.

Хотим напомнить о том что…

Что бы Вам стало легче определить, какой вид транспорта выбрать для доставки, надо рассчитать объем груза в м3. Рассчитать объем груза в м3 очень просто, тут необходимо знать точные размеры, которые затем необходимо перемножить.

Единицы необходимо пе6реводить именно в м3, иначе не получится посчитать доставку.

А что делать, если форма коробки не прямоугольная, а округлая? Ведь это большая редкость, но все же бывает.

Можно объем посчитать коробки или ёмкости в основании которых лежит круг, и для этого так же существует формула. Объем посчитать коробки формой круга позволяет выражение V *r2*h, размеры прежде всего надо безошибочно измерить.

Калькулятор объемов

Предоставляем к вашему вниманию калькулятор: объем грузов в м3, с помощью него вы можете самостоятельно делать расчёты. Калькулятор объем грузов расположен на наем сайте специально для вашего удобства, и для быстроты расчетов.

Для чего нужен калькулятор расчета объема груза?

Мы с вами деловые люди и потерянное время порой несёт в себе большие минусы. Хотите получать грузы быстро и надёжно? И при этом в максимально короткие сроки узнавать цены на их перевозку и доставку?

Вот именно здесь, поможет калькулятор объёма груза!

Наш калькулятор объёмов позволяет вам рассчитать объём груза в м3, поэтому вопрос о объёме коробки больше не возникнет. Калькулятор объёмов простой и удобный в применении, он выдаст результаты как объёма коробки так и груза.

Итак, с помощью калькулятора объёма Вы решаете несколько вопросов:

Как вычислить объем груза (или коробки)? Не забывайте о количественной единице, которую вы берёте в расчёт.

Как посчитать объем коробки в м3? Калькулятор сразу считает в международной системной единице, никакого перевода не требуется.

Как рассчитать кубатуру коробки (груза)? Помните, что кубатура — это число кубических единиц в объёме данного тела.

Столкнулись с одним из них или возник подобный? Наша компания рада предложить для Вашего удобства объем в метрах кубических коробки посчитать, с помощью удобного калькулятора. 

А напоследок, давайте вспомним математику!

Часто возникает вопрос: «как высчитать объем?», только вот объем чего: какой фигуры, какой формы, всё всегда по-разному. Как высчитать объем коробки и груза в целом – это интересует вас, ведь именно по этой причине Вы на сайте!

Какая проблема самая распространённая?

Многие путают то как вычислять объём плоских фигур и объемных, т. к., ошибаются в понятиях, точнее затрудняются с ответом. Как вычислять объём не надо знать, хватит того, что вы укажете размеры, главное не забывайте, что их 3.

Закончив все расчеты, остается еще одна задача.

После того, как рассчитать объем груза оказалось не проблемой, необходимо думать о том, какой вид доставки подобрать. Рассчитать объем груза для подборки транспорта Вам придётся точно, не допуская не каких ошибок и недочетов.

А какой Вам нужен транспорт?

Напомним, в доставке кроме того, как рассчитать кубатуру есть еще не менее важные вещи, например размещение товаров. Как рассчитать кубатуру вы знаете, поэтому всё остальное в ваших руках, теперь выбор транспорта зависит от вас.

 

 

Как посчитать площадь комнаты, стены, пола, потолка

Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты.  О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.  

Часто требуется посчитать кубатуру комнаты, ее объем

Содержание статьи

Площадь комнаты в квадратных метрах

Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:

• Рулетка. Лучше — с фиксатором, но подойдет и обычная.
• Бумага и карандаш или ручка.
• Калькулятор (или считайте в столбик или в уме).

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м.  В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

Площадь комнаты сложной формы

Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):

1. Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
2. Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
3. Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров.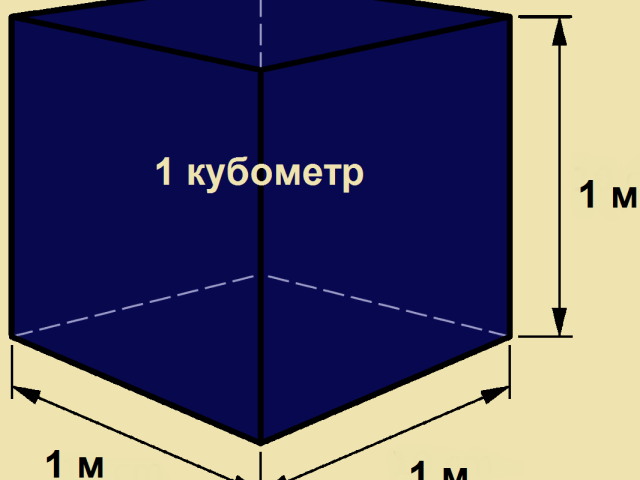 Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.

Как посчитать площадь комнаты неправильной формы

В этом случае порядок вычислений такой:

1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
2. Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
3. Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
4. Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

Формулы расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины.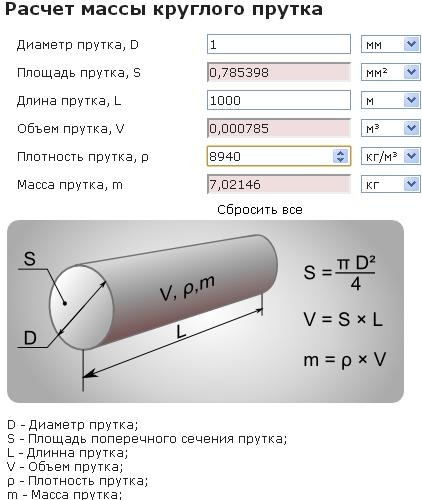 Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

• высота потолков;
• высота и ширина дверных проемов;
• высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

Удобнее всего размеры наносить на план

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

1. Стена с дверью:
   • 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
   • сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
   • стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
2. Стена с окном:
   1. квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
   2. сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
   3. стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.

Объем комнаты

Формула расчета объема комнаты

Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:

• длинна — 5,6 м;
• ширина — 3,2 м;
• высота — 2,5 м.

Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м³.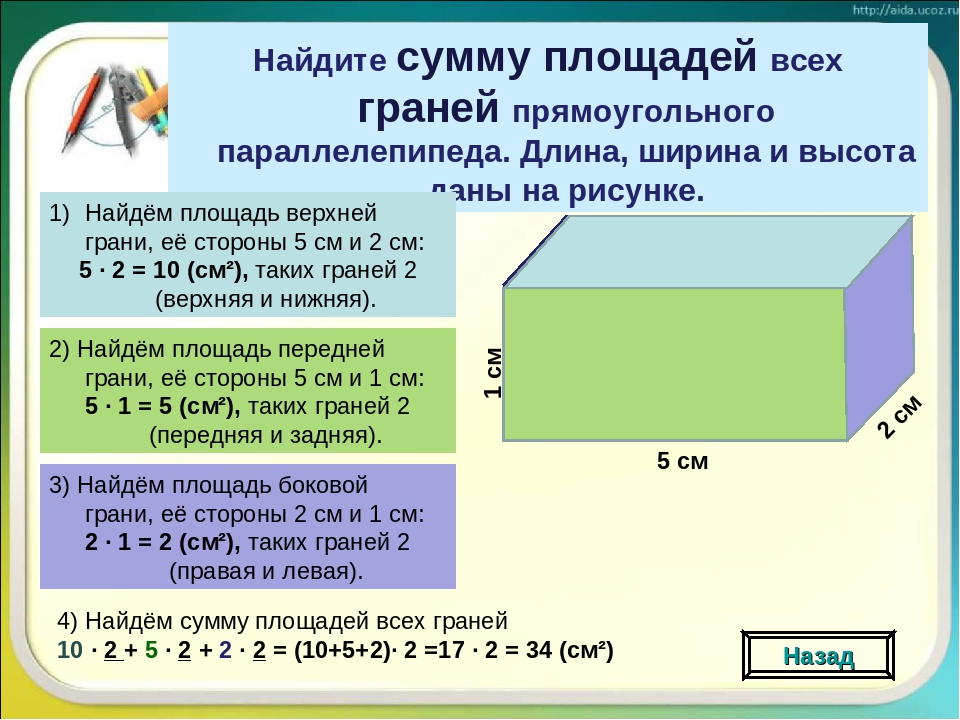 Итак, объем помещения 44,8 куба.

 

Калькулятор расчёта площади комнаты, расчет площади пола и потолка

Приведу пример расчета пола или потолка комнаты (кухни) в квадратных метрах.

Формула расчета простая, S = a*b, где S — площадь, а и b — соответственно, длина и ширина комнаты.

В нашем примере (рисунка с обмерами) вместо маленьких букв длина — А и ширина — Б., и противоположенных стен — Г и В.

Чтобы рассчитать площадь комнаты по полу:

— если у нас длина комнаты 5 метра, а ширина 3 метров, тогда нам надо ( 5*3 = 15 кв.м.), в итоге получаем 15 кв.м. по полу

 

 

 

 

Воспользуйтесь нашим Калькулятором, чтобы расчитать площадь пола или потолка

Если вы не хотите в ручную рассчитывать площадь пола или вы, что то не поняли при описание расчетов, то вы можете воспользоваться нашим калькулятором и рассчитать площадь пола или потолка автоматически.

Для расчёта необходимо измерить в метрах длину, ширину комнаты и внести данные по порядку заполнив форму и вы автоматически получите расчет площади пола или потолка в квадратных метрах.

 

Калькулятор расчёта площади пола

 

 

Примечание:

Обращаем ваше внимание, что измерения необходимо проводить в метрах. Т.е. если вы получили длину комнаты 964 сантиметров, то в поля формы необходимо ввести значение 9.64. Обратите внимание, что дробные числа нужно вводить с точкой, а не с запятой!

Т.е. 2,6 — неправильно, 2.6 — правильно

Калькулятор рассчитывает не только площадь пола или потолка, данный калькулятор можно также использовать для расчёта площади любых других прямоугольных объектов у которых есть длина и ширина. В этом случае вместо ширины и длины комнаты вам необходимо подставить значения ширины и длины этих самых объектов (окна, двери и т. д.,) к примеру таких как площадь окон и дверей.

К примеру как можно проверить и расчитать в ручную площадь окон и дверей.:

— если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров.

— а двери ширина 0,8 метров, а высота 2,05 метров.

Окно: (1,6*1,5)= 2,4 кв.м., в итоге окно получаем 2,4 кв.м.,

Двери: (0,8*2,05)= 1,64 кв.м, в итоге двери получаем 1,64 кв.м.,

 

 

Чтобы рассчитать площадь комнаты по стенам: воспользуйтесь нашим Калькулятором, чтобы расчитать площадь стен

 

Источник: remont-otdelka-m.ru

Как рассчитать квадратные метры стен комнаты, расчет площади стен

Приведу пример расчета пола и стен комнаты (кухни) в квадратных метрах.

Формула расчета простая, S = a*b, где S — площадь, а и b — соответственно, длина и ширина комнаты.
В нашем примере (рисунка с обмерами) вместо маленьких букв длина — А и ширина — Б.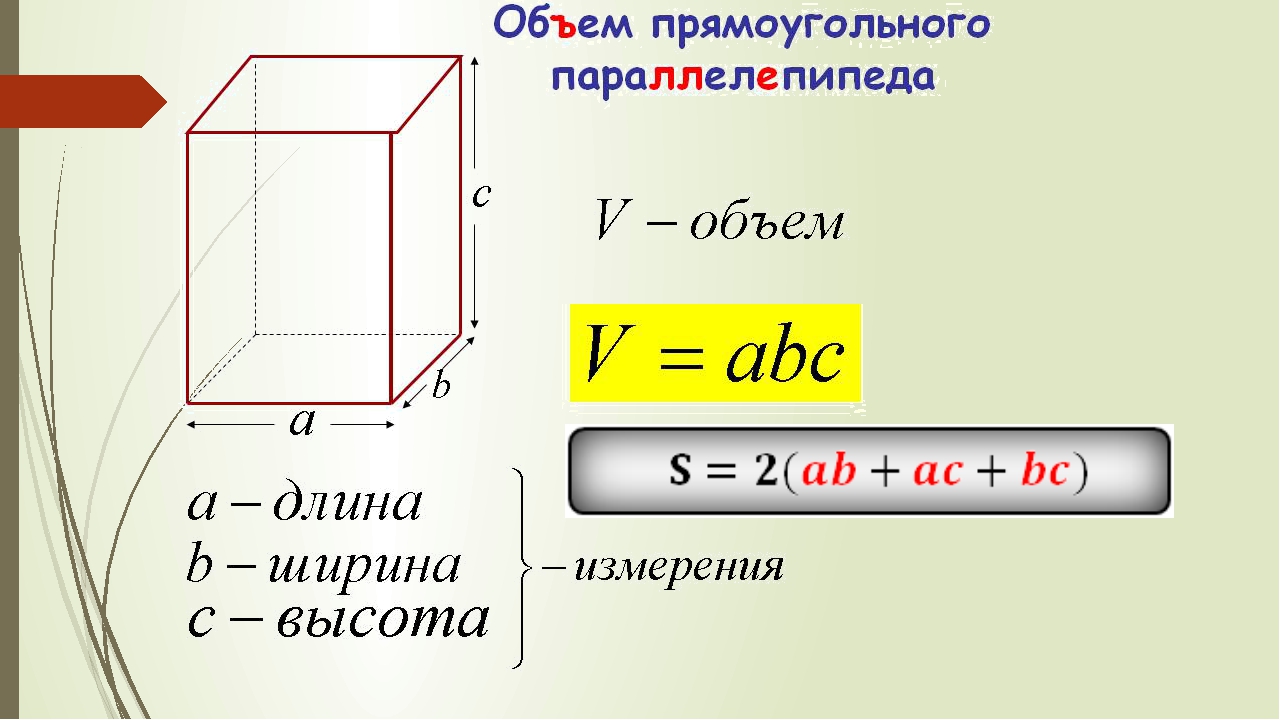 , и противоположенных стен — Г и В.

Чтобы рассчитать площадь комнаты по полу:

— если у нас длина комнаты 5 метра, а ширина 3 метров, тогда нам надо ( 5*3 = 15 кв.м.), в итоге получаем 15 кв.м. по полу

Чтобы рассчитать площадь комнаты по стенам:

Надо с начало сложить длины всех четырех сторон комнаты А + Б + Г + В и умножить на высоту потолка комнаты h, ( А + Б + Г + В)* h
— если у нас длина комнаты 5 метра, а ширина 3 метров, а высота потолка комнаты к примеру 2,5 метра, тогда надо ((5+3+5+3)*2,5= 40 кв.м.), в итоге получаем 40 кв.м. по стенам.

Но это еще не все, для того чтобы получить чистые квадратные метры стен комнаты для ремонта и отделки квартиры, надо из полученного вычесть двери и окно.

К примеру:

— если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров.
— а двери ширина 0,8 метров, а высота 2,05 метров.

Окно: (1,6*1,5)= 2,4 кв.м., в итоге окно получаем 2,4 кв.м.,
Двери: (0,8*2,05)= 1,64 кв.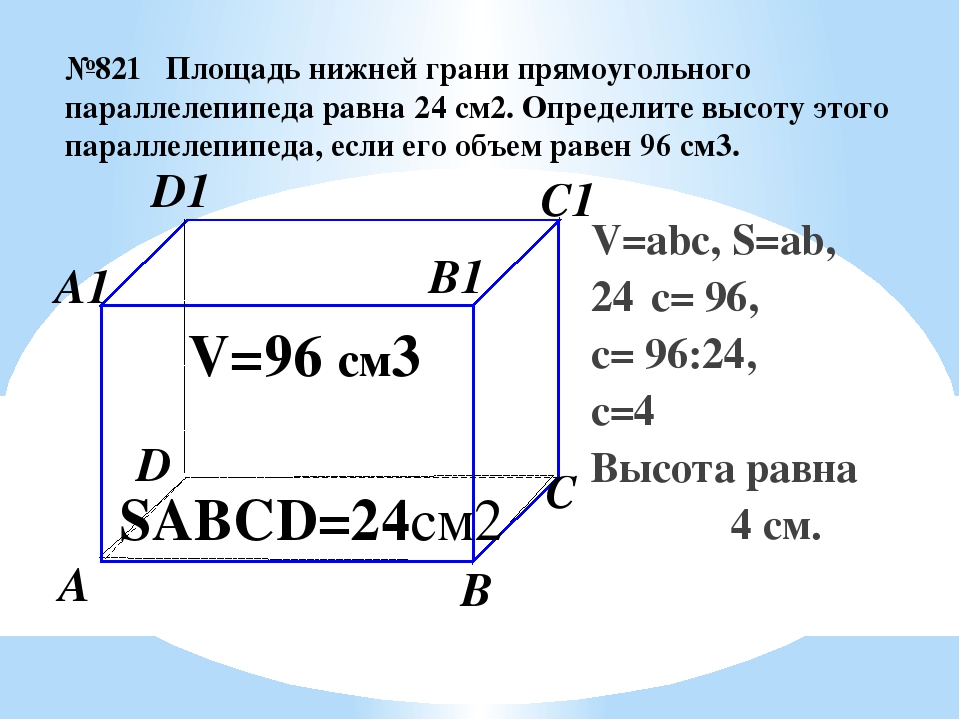 м, в итоге двери получаем 1,64 кв.м.,

Осталось вычесть от (40-2,4-1,64)= 35,96 кв.м.,
ИТОГО: Получили 35,96 кв.м. по стенам комнаты.

 

 

Если вы не хотите в ручную рассчитывать площадь стен или вы, что то не поняли при описание расчетов, то вы можете воспользоваться нашим калькулятором и рассчитать площадь стен автоматически.

Для расчёта необходимо измерить в метрах длину, ширину комнаты и высоту потолка и внести данные по порядку заполнив форму и вы автоматически получите расчет площади стен в квадратных метрах.

 

Калькулятор расчёта площади стен

 

Примечание:

Обращаем ваше внимание, что измерения необходимо проводить в метрах. Т.е. если вы получили длину комнаты 964 сантиметров, то в поля формы необходимо ввести значение 9.64. Обратите внимание, что дробные числа нужно вводить с точкой, а не с запятой!

Т.е. 2,6 — неправильно, 2.6 — правильно

Калькулятор рассчитывает только площадь стен, но без учета и вычета площади окон и дверей, для этого надо еще раз повторить расчеты на площадь окон и дверей описанные выше.

К примеру:

— если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров.
— а двери ширина 0,8 метров, а высота 2,05 метров.

Окно: (1,6*1,5)= 2,4 кв.м., в итоге окно получаем 2,4 кв.м.,
Двери: (0,8*2,05)= 1,64 кв.м, в итоге двери получаем 1,64 кв.м.,

Осталось вычесть от (от полученных расчетов автоматического калькулятора (площадь чистых стен) -2,4-1,64 (Окно и двери)= получим площадь стен с учетом вычета Окон и двери помещения (комнаты) в кв.м.,

 

 

Чтобы рассчитать площадь комнаты по полу: воспользуйтесь нашим Калькулятором, чтобы расчитать площадь пола или потолка.

Калькулятор рассчитывает не только площадь пола или потолка, а также данный калькулятор можно использовать для расчёта площади любых других прямоугольных объектов у которых есть длина и ширина. В этом случае вместо ширины и длины комнаты вам необходимо подставить значения ширины и длины этих самых объектов (окна, двери и т.д.,) к примеру таких как площадь окон и дверей.

 

Источник: remont-otdelka-m.ru

Как рассчитать объем картонной коробки зная ее размеры

Чтобы правильно выбрать картонные коробки для конкретного груза, необходимо предварительно рассчитать ее объем. Эта величина максимально отображает вместимость гофротары.

Расчет объема коробок

Картонные коробки имеют квадратную или прямоугольную форму. В этом случае они представляют собой параллелепипед. Из школьного курса нам известно, что для расчета объема этой фигуры необходимы длина, ширина и высота. Размеры можно измерить с помощью обычной линейки или рулетки.

Расчет объема, исходя из размера коробки, можно произвести по формуле:

Формула для подсчета:
V=a*b*h.
Где a – длина основания (мм),
b – ширина основания (мм),
h — высота коробки (мм),
V — объем (л).

Эта формула представляет собой расчет объема параллелепипеда. Поэтому, ее можно использовать только для прямоугольных коробок.

Для тех случаев, когда тара имеет нестандартную форму, вычислить ее объем можно по формуле:

Формула для подсчета:
V=S*h.
Где S – площадь основания, которую рассчитывают в зависимости от его формы. В случае треугольного, шестиугольного или восьмиугольных оснований расчет площади выполняется по разным формулам.

Поскольку, единицей объема в международной системе измерений (СИ) являются кубические метры (м³), то более правильно размер длины, ширины и высоты перевести в метры. Для тех, кто привык работать с сантиметрами или миллиметрами, можно оставить эту размерность. Но при расчете объема груза придется использовать только ее.

Внутренний и внешний объем коробки

Зная точный объем гофрокороба, можно без затруднений подобрать подходящий груз. Для этого по той же методике следует вычислить его объем. Если груз имеет сложную конфигурацию, то для расчетов нужно использовать габаритные размеры. Понятно, что объем тары должен быть немного больше.

При выборе груза нужно также учитывать, на основании внутренних или внешних размеров был рассчитан объем коробок. Результаты будут несколько отличаться. В некоторых случаях это может иметь значение.

По этой причине для точного определения допустимых размеров груза желательно использовать внутренние размеры тары. Габариты ящиков и грузов должны отличаться между собой на 5-10 мм. Наружные размеры коробок необходимы при заполнении кузова автотранспорта для их перевозки. Они могут также потребоваться при вычислении требующейся площади склада для хранения.

Пошаговая инструкция для вычисления объема

Мы ознакомились с необходимыми теоретическими сведениями по расчету объема коробки. Рассмотрим описанные выше действия пошагово.

Измеряем длину коробки. Под ней подразумевают размер самой длинной стороны основания. Используем для этого рулетку или линейку. Переводим полученный размер в метры и записываем. Для небольшой тары измерения проще проводить в сантиметрах или миллиметрах. Если вы решили использовать одну из этих размерностей, примите во внимание, что остальные размеры, в том числе и габариты груза, нужно измерять в той же размерности.

Измеряем ширину коробки. Это размер более короткой стороны основания. Применяем те же единицы измерения. Записываем или запоминаем полученный результат. Для полностью квадратных коробок длина и ширина совпадают.

Далее необходимо измерить высоту нашей тары. Под высотой понимают сторону, расположенную перпендикулярно основанию. Проще говоря, это расстояние от нижнего клапана коробки до верхнего.

На следующем этапе в соответствии с формулой вычисления объема все полученные размеры перемножаем. Если в процессе измерений мы выявили, что размер нашей коробки 100х200х300 мм, то объем в этом случае представляет собой произведение всех трех величин. V=100х200х300=6 000000 мм³ или 0,006 м³.

В некоторых случаях существует необходимость перевести полученную величину в литры (л). Знание количества кубических единиц дает возможность понять, сколько таких кубов можно вместить внутри конкретной коробки. При расфасовке жидких, мелких или сыпучих товаров, которые занимают полный объем тары, необходимо это значение выразить в литрах. Для этого используем соотношение 1 м³ = 1000 л. В нашем случае V = 0,006х1000=6 л.

Напоминаем, что эту методику можно применять только для картонных изделий прямоугольной или квадратной формы. Для других случаев придется вспомнить школьный курс геометрии более глубоко. Используйте формулу для нахождения площади многоугольника. По ней сможете вычислить площадь основания вашей тары. Умножив ее на высоту, легко получите величину объема.

Калькулятор объема

Ниже приводится список калькуляторов объема для нескольких распространенных форм. Заполните соответствующие поля и нажмите кнопку «Рассчитать».

Калькулятор объема сферы

Калькулятор объема конуса

Калькулятор объема куба

Калькулятор объема цилиндра

Калькулятор объема прямоугольного резервуара

Калькулятор объема капсулы

Калькулятор объема сферической крышки

Для расчета укажите любые два значения ниже.

Калькулятор объема конической ствола

Калькулятор объема эллипсоида

Калькулятор объема квадратной пирамиды

Калькулятор объема трубки

Калькулятор площади сопутствующих поверхностей | Калькулятор площади

Объем — это количественная оценка трехмерного пространства, которое занимает вещество.Единица измерения объема в системе СИ — кубический метр, или м ³ . Обычно объем контейнера — это его вместимость и количество жидкости, которое он может вместить, а не количество места, которое фактически вытесняет контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы могут быть разбиты на более простые совокупные формы, а сумма их объемов используется для определения общего объема. Объемы других, еще более сложных фигур можно рассчитать с помощью интегрального исчисления, если существует формула для границы фигуры.Помимо этого, формы, которые нельзя описать известными уравнениями, можно оценить с помощью математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.

Сфера

Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, которые равноудалены от данной точки в ее центре, где расстояние между центром и любой точкой на сфере составляет радиус r .Вероятно, самый известный сферический объект — это идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и расчет их объемов одинаков. Как и в случае с кругом, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема шара приведено ниже:

EX: Клэр хочет заполнить идеально сферический воздушный шар с радиусом 0.15 футов с уксусом, чтобы использовать его в борьбе с ее заклятым врагом Хильдой на воздушных шарах в предстоящие выходные. Необходимый объем уксуса можно рассчитать, используя приведенное ниже уравнение:

объем = 4/3 × π × 0,15 ³ = 0,141 фута ³

Конус

Конус — это трехмерная форма, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус формируется аналогично окружности набором отрезков прямой, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или другое основание).На этой странице рассматривается только случай конечного правого кругового конуса. Конусы, состоящие из полуосей, некруглых оснований и т. Д., Которые простираются бесконечно, не рассматриваются. Уравнение для расчета объема конуса выглядит следующим образом:

, где r — радиус, а h — высота конуса

EX: Би полна решимости выйти из магазина мороженого, не зря потратив свои с трудом заработанные 5 долларов. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, несомненно, больше.Она определяет, что на 15% предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15% больше, чем вафельный рожок. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью следующего уравнения:

объем = 1/3 × π × 1,5 ² × 5 = 11,781 дюйм ³

Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет <15%, и решает купить сахарный рожок.Теперь все, что ей нужно сделать, это использовать свой ангельский детский призыв, чтобы заставить посох выливать мороженое из контейнеров в ее рожок.

Куб

Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых пересекаются в каждой из его вершин, и все они перпендикулярны своим соответствующим смежным граням. Куб является частным случаем многих классификаций геометрических фигур, включая квадратный параллелепипед, равносторонний кубоид и правый ромбоэдр.Ниже приведено уравнение для расчета объема куба:

объем = ³
где a — длина ребра куба

EX: Боб, который родился в Вайоминге (и никогда не покидал штат), недавно посетил свою исконную родину Небраску. Пораженный великолепием Небраски и окружающей средой, непохожей на какие-либо другие, с которыми он когда-либо сталкивался, Боб знал, что ему нужно привезти с собой домой часть Небраски. У Боба есть чемодан кубической формы с длиной по краям 2 фута, и он рассчитывает объем почвы, который он может унести с собой домой, следующим образом:

объем = 2 ³ = 8 футов ³

Цилиндр

Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от данной прямой оси.Однако в обычном использовании «цилиндр» относится к правильному круговому цилиндру, где основания цилиндра представляют собой окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . Уравнение для расчета объема цилиндра показано ниже:

объем = πr ² ч
где r — радиус, а h — высота резервуара

EX: Кэлум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником рециркуляции, он извлек три цилиндрических бочки с незаконной свалки и очистил бочки от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя следующее уравнение:

объем = π × 3 ² × 4 = 113.097 футов ³

Он успешно построил замок из песка в своем доме и в качестве дополнительного бонуса ему удалось сэкономить электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте.

Прямоугольный бак

Прямоугольный резервуар — это обобщенная форма куба, стороны которого могут иметь разную длину. Он ограничен шестью гранями, три из которых пересекаются в его вершинах, и все они перпендикулярны своим соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:

объем = длина × ширина × высота

EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к торту.Она планирует отправиться в поход по тропе Калалау на Кауаи, и, хотя она в очень хорошей форме, Дарби беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет набить свою идеально прямоугольную упаковку длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может уместить в свою упаковку, рассчитан ниже:

объем = 2 × 3 × 4 = 24 фута ³

Капсула

Капсула — это трехмерная геометрическая форма, состоящая из цилиндра и двух полусферических концов, где полусфера — это полусфера.Отсюда следует, что объем капсулы можно рассчитать, объединив уравнения объема для сферы и правого кругового цилиндра:

объем = πr 2 ч +

πr 3 = πr 2 (

р + з)

, где r — радиус, а h — высота цилиндрической части

EX: Имея капсулу радиусом 1,5 фута и высотой 3 фута, определите объем растопленного молочного шоколада, который Джо может нести в капсуле времени, которую он хочет похоронить для будущих поколений на своем пути к самопознанию. Гималаи:

объем = π × 1.5 ² × 3 + 4/3 × π × 1,5 ³ = 35,343 фута ³

Сферический колпачок

Сферический колпачок — это часть сферы, отделенная от остальной сферы плоскостью. Если плоскость проходит через центр сферы, сферический колпачок называется полусферой. Существуют и другие различия, включая сферический сегмент, где сфера сегментирована двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для расчета объема сферической крышки выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, указанной в калькуляторе:

Имея два значения, предоставленный калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:

Для r и R : h = R ± √R ² — r ²

Для R и h : r = √2Rh — h ²
где r — радиус основания, R — радиус сферы, а h — высота сферической крышки.

EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, решает саботировать мяч для гольфа Джеймса.Он отрезает идеальную сферическую крышку от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимый для замены сферической крышки и перекоса веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:

объем = 1/3 × π × 0,3 ² (3 × 1,68 — 0,3) = 0,447 дюйма ³

К несчастью для Джека, за день до игры Джеймс получил новую партию мячей, и все усилия Джека оказались напрасными.

Коническая Frustum

Усеченный конус — это часть твердого тела, которая остается при разрезании конуса двумя параллельными плоскостями. Этот калькулятор рассчитывает объем специально для правильного кругового конуса. Типичные конические усики, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы для питья. Объем усеченного правого конуса рассчитывается по следующей формуле:

объем =

πh (r 2 + rR + R 2 )

где r и R — радиусы оснований, h — высота усеченного конуса

EX: Би успешно приобрела мороженое в сахарном рожке и только что съела его таким образом, чтобы мороженое оставалось упакованным внутри рожка, а поверхность мороженого была ровной и параллельной плоскости отверстия рожка.Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть дна рожка, которая идеально параллельна ранее единственному отверстию. Теперь у Би есть усеченная пирамида правой конической формы, из которой вытекает мороженое, и ей необходимо рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма с радиусом 1,5 дюйма и 0,2 дюйма:

объем = 1/3 × π × 4 (0,2 ² + 0,2 × 1,5 + 1,5 ² ) = 10.849 из ³

Эллипсоид

Эллипсоид является трехмерным аналогом эллипса и представляет собой поверхность, которую можно описать как деформацию сферы посредством масштабирования элементов направления. Центр эллипсоида — это точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки линии, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным.Уравнение для расчета объема эллипсоида выглядит следующим образом:

, где a , b и c — длины осей

EX: Хабат любит есть только мясо, но его мать настаивает на том, что он ест слишком много, и позволяет ему есть столько мяса, сколько он может уместить в булочке в форме эллипса. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может уместить в своем сэндвиче. Учитывая, что его булочка имеет длину оси 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат рассчитывает объем мяса, который он может уместить в каждой полой булочке, следующим образом:

объем = 4/3 × π × 1.5 × 2 × 5 = 62,832 дюйма ³

Квадратная пирамида

Пирамида в геометрии — это трехмерное твердое тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это форма на плоскости, ограниченная конечным числом отрезков прямой. Существует много возможных многоугольных оснований пирамиды, но квадратная пирамида — это пирамида, в которой основание представляет собой квадрат. Еще одно отличие пирамид заключается в расположении вершины. У правых пирамид есть вершина, которая находится прямо над центром тяжести ее основания.Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды может быть записан как:

Объем обобщенной пирамиды:

, где b — площадь основания, а h — высота

Объем квадратной пирамиды:

, где a — длина края основания

EX: Ван очарован Древним Египтом и особенно любит все, что связано с пирамидами.Будучи старшим из своих братьев и сестер Ту, Дерево и Форе, он может легко загонять и развертывать их по своему желанию. Воспользовавшись этим, Ван решает воссоздать древнеегипетские времена, а его братья и сестры выступают в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать, используя уравнение для квадрата. пирамида:

объем = 1/3 × 5 ² × 12 = 100 футов ³

Трубчатая пирамида

Трубка, часто также называемая трубой, представляет собой полый цилиндр, который часто используется для передачи жидкостей или газа.Для вычисления объема трубы используется та же формула, что и для цилиндра (объем = pr ² h ), за исключением того, что в этом случае используется диаметр, а не радиус, и длина, а не высота. Таким образом, формула включает измерение диаметров внутреннего и внешнего цилиндров, как показано на рисунке выше, вычисление каждого из их объемов и вычитание объема внутреннего цилиндра из объема внешнего. С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:

, где d ₁ — внешний диаметр, d ₂ — внутренний диаметр, а l — длина трубы

EX: Beulah посвящен охране окружающей среды.Ее строительная компания использует только самые экологически чистые материалы. Она также гордится тем, что удовлетворяет потребности клиентов. У одного из ее клиентов есть загородный дом, построенный в лесу через ручей. Он хочет облегчить доступ к своему дому и просит Беулу построить ему дорогу, следя за тем, чтобы ручей мог течь свободно, чтобы не мешать его любимому месту рыбалки. Она решает, что надоедливые бобровые дамбы будут хорошей отправной точкой для прокладки трубы через ручей. Объем запатентованного бетона с низкой ударопрочностью, необходимый для строительства трубы с внешним диаметром 3 фута и внутренним диаметром 2.5 футов и длина 10 футов можно рассчитать следующим образом:

объем = π ×

× l0 = 21,6 футов 3

Единицы измерения общего объема

16000

0009

,7000

7000

28 10 ^{150009 Sciencing}

Обновлено 22 декабря 2020 г.

Крис Дезиел

Когда вы видите M3, вы можете думать о конкретной модели BMW, но в большинстве случаев это, вероятно, относится к тому.3, м ³ и (на почте) м.куб.

Кубический метр — довольно большая единица объема. Это равно 264 галлонам США, или примерно 20 заправкам вашего BMW M3.

Несмотря на то, что вы можете преобразовать любое измерение объема в кубические метры, вы не захотите использовать м3 для небольшого количества, для которого унции или кубические сантиметры будут более подходящими. Кубические метры также не подходят для средних измерений, таких как банки, баллоны или газовые баллоны.Литры и галлоны лучше.

Единственное место, где вы действительно видите м3, — это транспортировка, где общее сокращение для кубических метров — куб.м. Кубические метры — это метрические единицы, и если вы живете в Соединенных Штатах, вы, вероятно, будете измерять размеры участков в футах и ​​дюймах, поэтому вам нужно будет выполнить пересчет. У грузоотправителя, вероятно, будет калькулятор м3, который поможет вам в этом.

Калькулятор M3 с использованием метрических измерений

Чтобы вычислить объем контейнера, вам понадобится формула, которая связывает его размеры с его объемом.Наиболее распространенные из них перечислены ниже:

• Прямоугольная коробка : длина × ширина × высота
• Кубическая коробка : длина ³
• Сферический контейнер : 4π × радиус ³
• Цилиндрический контейнер : длина 4π × радиус ²
• Конический контейнер : длина π / 3 × радиус ²

Если вы измеряете размеры в метрах, вы напрямую получаете объем в м3.Если вы измеряете в сантиметрах, легко преобразовать в метры. Просто умножьте каждое измерение на 0,01, чтобы выразить его в метрах. Затем, используя формулу кубического метра, вы получите объем в м3.

Пример : Размер коробки 10 см × 20 см × 25 см. Каков его объем в м3?

Чтобы преобразовать сантиметры в метры, умножьте каждое на 0,01. Размеры коробки тогда составляют 0,1 м, 0,2 м и 0,25 м. Тогда объем будет:

(0,1 \ 0,2 \ умножить на 0.3

Использование единиц преобразования объема из имперской системы в метрическую

Пока люди в Соединенных Штатах продолжают измерять расстояние в дюймах, футах и ​​милях, люди в остальном мире должны будут знать, как преобразовывать эти единицы измерения в имперскую систему. единиц и их метрических аналогов. Предполагая, что вам нужно выразить объем в м3, а не в литрах, вы можете рассчитать объем в кубических дюймах, кубических футах или галлонах и преобразовать его в м3, используя следующие коэффициенты преобразования:

• 1 кубический дюйм = 1.64 × 10 ^-5 м ³
• 1 кубический фут = 0,024 м ³
• 1 галлон = 0,0038 м ³

Пример : A Размер посылки 12 × 18 × 20 дюймов. Как с помощью формулы кубического метра выразить его объем в кубометрах в почтовом отделении?

Один из способов сделать это — вычислить объем в кубических дюймах и преобразовать дюймы в куб. Тогда объем (12 × 18 × 20) = 4320 куб.{-5} = 0,71 \ text {cbm}

Преобразовать британские в метрические, затем использовать формулу кубического метра

Если вы производите измерения в британских единицах, альтернативным способом вычисления объема в м3 является преобразование измерений длины до метров, прежде чем использовать формулу объема. Для этого вам понадобятся следующие коэффициенты пересчета:

• 1 дюйм = 0,0254 метра
• 1 фут = 0,31 метра

Пример: в приведенном выше примере размер окна составляет 12 дюймов. × 18 дюймов × 20 дюймовВы можете преобразовать эти размеры в метры, используя соответствующий коэффициент преобразования. Измерения станут 12 (0,0254) × 18 (0,0254) × 20 (0,0254) = 0,31 м × 0,46 м × 0,51 м. Таким образом, объем составляет 0,73 куб.

Это немного отличается от объема, рассчитанного с использованием предыдущего метода, из-за округления.

Как рассчитать кубические метры

Обновлено 28 января 2020 г.

Кевин Бек

Проверено: Lana Bandoim, B.S.

Что такое кубический метр ? Даже когда вы читаете, вполне вероятно, что вашему разуму трудно понять, какую физическую ценность или количество это представляет.Даже если вы знаете, что кубические метры (м ³ ) представляют собой единицу объема в физической науке, вам может быть трудно вообразить кубический метр.

Метрическая система

Метрическая система, также называемая СИ или международной системой единиц, была разработана в 18 веке и внедрена в Европе в 1790-х годах. Его основная цель заключалась в замене неточных и неудобных единиц измерения футов, дюймов и т. Д. На единицы, с которыми было проще работать и которые основывались на абсолютных стандартах.

Таким образом, метр был выбран так, чтобы представлять одну десятимиллионную предполагаемого расстояния от экватора до Северного полюса, а килограмм был выбран как масса одного литра воды. Литр, в свою очередь, определялся как объем, занимаемый пространством в форме куба 0,1 м (10 сантиметров или см) на стороне или эквивалентным объемом в любой другой твердой форме.

Эти определения были изменены по сравнению с их исходными значениями только для того, чтобы отразить появление все более точных измерительных инструментов с течением времени.

Использование кубометра

Кубический метр — это пространство в форме куба со стороной 1 м или его эквивалента. Например, прямоугольная коробка длиной 2 м, шириной 1 м и высотой 0,5 м будет иметь объем 1 м ³ (1 × 2 × 0,5 = 1).

Кубический метр также называется stere , хотя это в значительной степени стало древним термином и не является приемлемым термином сам по себе в системе СИ. Он до сих пор используется для измерения штабелей обрезной древесины в деревообрабатывающей промышленности.

Стерео или кубический метр эквивалентен 35,315 кубическим футам ( ³ футов) или 0,276 корду , другому термину в лесной промышленности. Довольно легко представить себе ряд бревен шириной чуть более 1 фута, 10 футов длиной и 3 фута высотой; это сработает примерно на стереозвук.

Примеры расчета кубометра

1. Каков объем аквариума длиной 20 м, шириной 20 м и глубиной 10 м?

Расчет прост: 20 × 20 × 10 = 4000 м ^3. Что примечательно, так это огромная масса воды внутри. Если вспомнить, что 1 л воды имеет массу 1 килограмм, то кубический метр, который в 10 раз больше по бокам, чем литр, вмещает 1000 кг воды. Это более 2200 фунтов и называется метрической тонной или тонны . Для сравнения: традиционный тонны стоит ровно 2000 фунтов.

Объем воды 4000 м3 ³ , таким образом, имеет массу 4000 тонн или около 4400 тонн. Представьте себе прочность стекла, необходимого для удержания всего этого, не говоря уже об обитателях!

2.Вам дается гигантский шар шириной 2 м (около шести с половиной футов). Сколько воздуха может удерживать этот мяч, когда он полностью надут? То есть каков его объем?

Чтобы решить, вам нужно только знать или ссылаться на объем сферы и понимать, что вы можете рассматривать мяч как таковой для целей физической задачи. Этот объем определяется формулой V = 4πr ³ . Поскольку шар имеет диаметр 2 м, его диаметр составляет 2 м, а значит, и радиус 1 м. Таким образом, объем этого шара равен (4π) (1) 2 = 4π м ³ , или 12.57 м ³ .

Калькулятор кубических метров

Вы можете использовать любое количество онлайн-калькуляторов, чтобы с легкостью работать с кубическими метрами и другими единицами объема. Пример такого инструмента можно найти в Ресурсах. Это позволяет вам ввести значение в общей единице объема, такой как галлон, или в менее распространенной единице, такой как кубический ярд, и вернуть число, дающее эквивалент в кубических метрах.

Калькулятор объема. Определение | Формулы

Калькулятор объема вычислит объем некоторых из наиболее распространенных трехмерных твердых тел.Прежде чем мы перейдем к тому, как рассчитать объем, вы должны знать определение объема. Объем отличается от площади, которая представляет собой объем пространства, занимаемого двухмерной фигурой. Поэтому вы можете быть сбиты с толку относительно того, как найти объем прямоугольника по сравнению с тем, как найти объем коробки. Калькулятор поможет вычислить объем сферы, цилиндра, куба, конуса и прямоугольных тел.

Что такое объем? Определение объема

Объем — это объем пространства, который занимает объект или вещество.Как правило, под объемом контейнера понимается его вместимость, а не пространство, которое сам контейнер перемещает. Кубический метр (м ³ ) — это единица измерения объема в системе СИ.

Однако термин том может также относиться ко многим другим вещам, например,

• степень громкости или интенсивность звука (вы можете проверить наш калькулятор шумового загрязнения или калькулятор дБ)
• количество или количество чего-либо (обычно большого количества)
• формальное слово для книги или одной из набора связанных книг.

Единицы объема, таблица пересчета

Популярные единицы объема:

1. Метрические единицы объема

• кубических сантиметра (см³)
• кубических метра (м³)
• литры (л, л)
• миллилитры (мл, мл)

2. Стандарт США, Великобритания

• жидкая унция (жидкая унция)
• кубический дюйм (у.е.)
• кубический фут
• чашки
• пинты (пт)
• кварты (кварты)
• галлона (гал)

Если вам нужно преобразовать единицы объема, вы можете использовать наш конвертер больших объемов.Еще один полезный инструмент — наш калькулятор граммов в чашки, который может помочь, если вы хотите использовать рецепт еды из другой страны. Обратите внимание, что это не простое преобразование, а переход от веса (граммов) к единице объема (чашки) — поэтому вам нужно знать тип ингредиента (или, точнее, его плотность).

Кроме того, вы можете взглянуть на эту аккуратную таблицу преобразования единиц объема, чтобы узнать коэффициент преобразования в мгновение ока:

Единица	кубических метров	миллилитров
миллилитров (кубических сантиметров)	0,000001	1
кубических дюймов	0,00001639	000473	473
кварта	0,000946	946
литр	0,001	1,000
галлон	0,0037817	5	5
кубических ярдов	0,764555	764,555
кубических метров	1	1,000,000
кубических километров	1,000,000,000

	кубических дюймов	кубических футов	кубических ярдов	галлонов жидкости сша	галлонов сухих сша	imp жидких галлонов	баррелей (нефть)	стаканов	жидких унций (Великобритания)	жидких унций (США)	пинт (Великобритания)
м3	6.1 10 4	35,3	1,30 8	264,2	227	220	6,29	4227	3,52 10 4	3,38 10 4	1760
кубический дециметр	61.02	0,035	1,3 10 -3	0,264	0,227	0,22	0,006	4,23	35,2	33,8	1,76
кубический сантиметр	0.061	3,5 10 -5	1,3 10 -6	2,64 10 -4	2,27 10 -4	2,2 10 -4	6,29 10 -6	4,2 10 -3	3,5 10 -2	3.34 10 -2	1,76 10 3
кубический миллиметр	6,1 10 -5	3,5 10 -8	1,31 10 -9	2,64 10 -7	2,27 10 -7	2,2 10 -7	6.3 10 -9	4,2 10 -6	3,5 10 -5	3,4 10 -5	1,76 10 -6
гектолитров	6,1 10 3	3,53	0,13	26.4	22,7	22	0,63	423	3,5 10 3	3381	176
литров	61	3,5 10 -2	1.3 10 -3	0,26	0,23	0,22	6,3 10 -3	4,2	35,2	33,8	1,76
сантилитров	0,61	3.5 10 -4	1,3 10 -5	2,6 10 -3	2,3 10 -3	2,2 10 -3	6,3 10 -5	4,2 10 -2	0,35	0,338	1.76 10 -2
миллилитров	6,1 10 -2	3,5 10 -5	1,3 10 -6	2,6 10 -4	2,3 10 -4	2,2 10 -4	6,3 10 -6	4.2 10 -3	3,5 10 -2	3,4 10 -2	1,76 10 -3
кубических дюймов	1	5,79 10 -4	2,1 10 -5	4,3 10 -3	3.7 10 -3	3,6 10 -3	10 -4	6,9 10 -2	0,58	0,55	2,9 10 -2
кубических футов	1728	1	0.037	7,48	6,43	6,23	0,18	119,7	997	958	49,8
кубических ярдов	4,7 10 4	27	1	202	173.6	168,2	4,8	3232	2,69 10 4	2,59 10 4	1345
жидких галлонов сша	231	0,134	4,95 10 -3	1	0.86	0,83	0,024	16	133,2	128	6,7
галлонов США сухих	268,8	0,156	5,76 10 -3	1.16	1	0,97	0,028	18,62	155	148,9	7,75
imp жидких галлонов	277,4	0,16	5,9 10 -3	1.2	1,03	1	0,029	19,2	160	153,7	8
баррелей (нефть)	9702	5,61	0,21	42	36.1	35	1	672	5596	5376	279,8
стаканов	14,4	8,4 10 -3	3,1 10 -4	6.2 10 -2	5,4 10 -2	5,2 10 -2	1,5 10 -3	1	8,3	8	0,4
жидких унций (Великобритания)	1,73	10-3	3.7 10 -5	7,5 10 -3	6,45 10 -3	6,25 10 -3	1,79 10 -4	0,12	1	0,96	5 10 -2
жидких унций (США)	1.8	10 -3	3,87 10 -5	7,8 10 -3	6,7 10 -3	6,5 10 -3	1,89 10 -4	0,13	1,04	1	0.052
пинт (Великобритания)	34,7	0,02	7,4 10 -4	0,15	0,129	0,125	3,57 10 3	2,4	20	19.2	1

Как рассчитать объем? Формулы объема

На этот вопрос нет однозначного ответа, так как он зависит от формы рассматриваемого объекта. Вот формулы для некоторых наиболее распространенных форм:

1. Куб = с³ , где с — длина стороны.

2. Сфера = (4/3) πr³ , где r — радиус.

3. Цилиндр = πr²h , где r — радиус, а h — высота.

4. Конус = (1/3) πr²h , где r — радиус, а h — высота.

5. Прямоугольное тело (объем ящика) = lwh , где l — длина, w — ширина и h — высота (примером такой формы может служить простой бассейн).

6. Пирамида = (1/3) Ah , где A — площадь основания, а h — высота. Для пирамиды с правильным основанием также можно использовать другое уравнение: Пирамида = (n / 12) * h * длина_сокры ² * кроватка (π / n) , где n — количество сторон основания для правильный многоугольник.

7. Призма = πAh , где A — площадь основания, а h — высота. Для прямоугольной призмы уравнение можно легко вывести, как и для правой прямоугольной призмы, которая, по-видимому, имеет ту же форму, что и прямоугольник.

Ач

Форма	Имя	Формула
	Куб	В = с³
	Призма прямоугольная правая (прямоугольная, прямоугольная)	В = л / ч
	Призма или цилиндр	В =
	Пирамида или конус	В = Ач / 3
	Сфера	В = 4πr³ / 3

Калькулятор объема и инструменты, предназначенные для определенных форм

Мы решили сделать из этого калькулятора объема простой инструмент, охватывающий пять самых популярных трехмерных фигур.Однако не все уравнения объема и формы могут быть реализованы здесь, так как это сделает калькулятор перегруженным и не интуитивно понятным. Так что, если вы ищете конкретную форму, ознакомьтесь с калькуляторами, посвященными объемам выбранных форм:

Калькулятор объема

— как использовать

Давайте посмотрим на примере использования этого калькулятора объема:

1. Выберите тип 3D-формы . Если вы не можете найти форму, объем которой хотите рассчитать, выберите другие специальные специальные калькуляторы (ссылки вы найдете выше).В этом примере предположим, что вы хотите рассчитать объем цилиндра.

2. Выберите правую часть калькулятора объема . В нашем случае это деталь под названием Объем цилиндра .

3. Введите данные в соответствующие поля . Наш цилиндр имеет радиус 1 фут и высоту 3 фута. Вы можете изменить единицы измерения простым щелчком по названию единицы.

4. Поехали! Объем выбранной формы отображается .В нашем случае это 9,42478 куб. Футов

Если вы хотите проверить, сколько это в баррелях США, просто нажмите на название единицы и выберите бочки из раскрывающегося списка. Наш цилиндр вмещает ~ 2,24 баррелей масла.

Измерение объема твердых тел, жидкостей и газов

Как найти объем объектов с разным состоянием материи?

1. Цельный

Для обычных трехмерных объектов вы можете легко вычислить объем, измерив его размеры и применив соответствующее уравнение объема.Если это неправильная форма, вы можете попробовать сделать то же самое, что заставило Архимеда выкрикнуть знаменитое слово * Эврика *! Вероятно, вы слышали эту историю — Архимеда попросили выяснить, сделана ли корона Иеро из чистого золота или просто позолочена, но не сгибая и не разрушая ее. Идея пришла ему в голову, когда он принимал ванну — войдя в ванну, он заметил, что уровень воды поднялся. Из этого наблюдения он пришел к выводу, что объем вытесненной воды должен быть равен объему той части его тела, которую он погрузил в воду.Зная объем необычного объекта и его вес, он мог вычислить плотность и сравнить ее с плотностью чистого золота. Легенда гласит, что Архимед был так взволнован этим открытием, что выскочил из ванны и побежал голым по улицам Сиракуз.

Итак, если вы хотите измерить объем необычного объекта, просто следуйте по стопам Архимеда (хотя вы можете опустить часть «голая гонка»):

• Возьмите емкость больше, чем объект, объем которого вы хотите измерить, .Это может быть ведро, мерный стаканчик, химический стакан или мерный цилиндр. На нем должна быть шкала.

• Налейте воду в емкость и снимите показания объема.

• Поместите объект внутрь . Он должен быть полностью погружен для измерения всего объема объекта. Прочтите том. Этот метод не сработает, если ваш объект растворяется в воде.

• Разница между замерами — это объем нашего объекта.

Эти измерения необходимы для расчета выталкивающей силы, основанной на принципе Архимеда.

2. Жидкость

Обычно измерить объем жидкости довольно просто — все, что вам нужно, это какой-нибудь мерный сосуд с градуировкой. Выберите тот, который соответствует вашим потребностям: необходимо учитывать количество жидкости и степень точности. Емкости, используемые для выпечки торта (посмотрите отличный калькулятор для рецепта блинов), будут отличаться от тех, что используются в химии (например.грамм. в расчетах молярной концентрации) будет отличаться от тех, которые используются в медицинских целях (например, доза лекарства).

3. Газ

Мы должны использовать более сложные методы для измерения объема газа. Вы должны помнить, что на объем газа влияют температура и давление, и что газы расширяются, чтобы заполнить любой контейнер, в который они помещены. Вы можете попробовать измерить это:

• Надуйте баллон газом, который вы хотите измерить (например,г., с гелием, чтобы поднять вас в воздух). Затем можно воспользоваться методом Архимеда — опустить баллон в ведро с водой и проверить разницу объемов. Вы найдете подробные инструкции на странице wikihow.

• Проверьте показатели, связанные с объемом ваших легких, с помощью прибора под названием спирометр .

• В химии, газовый шприц используется для ввода или отбора объема газа из закрытой системы . Эту лабораторную посуду также можно использовать для измерения объема газа, выделяющегося в результате химической реакции.

Или рассчитать :

• Найдите объем газа , учитывая его плотность и массу . Используйте простое уравнение объема V = m / d .

• Рассчитайте объем сжатого газа в баллоне, используя уравнение идеального газа.

Как найти объем * прямоугольника * по сравнению с объемом * коробки *

Вы не можете рассчитать объем прямоугольника , объем круга или объем квадрата, потому что это двухмерные геометрические фигуры.Таким образом, прямоугольник не имеет объема (но имеет площадь). Вероятно, вы ищете объем прямоугольного кубоида (или, говоря более общим языком, вы хотите найти объем коробки), который представляет собой трехмерный объект.

Чтобы найти объем коробки, просто умножьте длину, ширину и высоту — и готово! Например, если размер коробки 5х7х2 см, то объем коробки составляет 70 кубических сантиметров.
Для размеров, которые представляют собой относительно небольшие целые числа, легко вычислить объем вручную.Для больших или десятичных чисел использование калькулятора объема очень эффективно.

В реальной жизни есть много приложений, в которых может пригодиться калькулятор объема. Один из таких примеров — строительство дорог или тротуаров, где должны быть построены бетонные плиты. Как правило, бетонные плиты представляют собой твердые тела прямоугольной формы, поэтому можно использовать калькулятор бетона, который является приложением калькулятора объема.

Также формулы объема могут быть полезны, если вы увлеченный садовник или просто счастливый обладатель дома с двором.Ознакомьтесь с нашими замечательными инструментами, такими как:

Более того, вы можете встретить объем на кухне или в ванной: у любой жидкости, которую мы пьем (например, воды в бутылках), а также косметических товаров или зубной пасты на упаковке продукта указан объем (в миллилитрах / литрах или жидких унциях / галлоны).

Еще одно родственное приложение, хотя и немного другое, — это концепция площади поверхности. Предположим, весь фасад здания должен быть окрашен. Чтобы знать, сколько нужно приобрести краски, необходимо рассчитать площадь здания.Удобный в использовании калькулятор площади рассчитает это за вас.

FAQ

Как найти объем?

Формула объема зависит от формы объекта . Одной из самых популярных форм является прямоугольная призма, также известная как коробка, где вы можете просто умножить длину на ширину на высоту , чтобы найти ее объем. Другой распространенной формой является цилиндр — чтобы найти его объем, умножьте высоту цилиндра на площадь его основания (π ⨉ r ² ).Для других трехмерных фигур проверьте Калькулятор объема Omni.

Как измерить объем?

Измерение объема зависит от состояния вещества вашего объекта. Для жидкостей вы можете использовать мерный цилиндр или бюретку для измерений в химической лаборатории или мерную чашку и ложку для повседневных целей. Что касается газов, чтобы приблизительно измерить объем, вы можете надуть баллон и использовать его для вытеснения воды в мерном цилиндре. Аналогичный метод работает для твердых тел — поместите объект в градуированный контейнер и измерьте изменение показаний.

Объем — квадрат или куб?

Объем «кубовидный», так как это трехмерная мера. Площадь — это «квадратное» значение, поскольку площадь фигуры охватывает два измерения. Вы можете вспомнить, что объем представляет собой кубическое значение, вспомнив несколько названий единиц объема, например, кубических метров , кубических футов или кубических ярдов .

Как рассчитать объем?

В зависимости от формы объекта вы можете использовать разные формулы для расчета объема:

• Объем куба = сторона ³ .
• Кубоид (прямоугольная коробка) объем = длина ⨉ ширина ⨉ высота
• Объем сферы = (4/3) ⨉ π ⨉ радиус ³
• Объем цилиндра = π ⨉ радиус ² ⨉ высота
• Объем конуса = (1/3) ⨉ π ⨉ радиус ² ⨉ высота
• Объем пирамиды = (1/3) ⨉ площадь основания ⨉ высота

В чем измеряется объем?

Кубический метр — единица объема в системе СИ.Однако, поскольку это непрактично, чаще всего вы можете встретить объем, выраженный в:

.

• Кубические сантиметры
• Кубические дюймы
• Миллилитры
• литров
• галлонов

Как найти объем жидкости?

Градуированные цилиндры и Колбы Эрленмейера подойдут, если вам нужно приблизительно измерить объем жидкости. Для более точных измерений нужно использовать мерную пипетку и бюретку.Однако, если вы печете торт или готовите вкусное блюдо и в рецепте используются единицы измерения объема, вы можете просто использовать мерный стакан, стакан или ложку.

Какая единица измерения объема в системе СИ?

Кубический метр (м ³ ) — это единица измерения объема в системе СИ. Он образован от основной единицы измерения длины в системе СИ — метра. Хотя кубический метр является основной единицей СИ, чаще используются другие единицы: для метрической системы популярны миллилитры, литры или кубические сантиметры, а для имперской системы вы можете найти объем, выраженный в пинтах, галлонах, кубических дюймах и т. Д. кубические футы или кубические ярды.

Объемный интенсивный или экстенсивный?

Объем — это обширное свойство , такое же, как количество вещества, массы, энергии или энтропии. Обширное свойство — это мера, которая зависит от количества вещества . Посмотрите на этот пример: стакан, бочка и бассейн, полный воды, имеют разные объемы и массы ( расширенных свойств ), но вода в этих трех контейнерах будет иметь одинаковую плотность, показатель преломления и вязкость ( интенсивных свойств ). ).

В чем разница между площадью поверхности и объемом?

Объем — это трехмерная мера , а площадь поверхности — двумерная . Объем сообщает нам о кубическом пространстве, которое занимает объект, а площадь поверхности — это сумма всех областей, образующих трехмерную форму. Возьмем, например, картонную коробку 📦:

• Объем — это объем места, занимаемого коробкой, то есть свободного места внутри коробки
• Площадь поверхности — это пространство , занимаемое сторонами коробки , вычисленное при покраске сторон или упаковке коробки в бумагу.

Как найти объем объекта неправильной формы?

Вы можете использовать метод вытеснения жидкости для твердых объектов неправильной формы:

1. Наполните емкость водой и отметьте уровень воды.
2. Бросьте ваш объект внутрь и снова отметьте уровень. Убедитесь, что ваш предмет не растворяется в воде.
3. Для масштабированных контейнеров вы можете всего лишь вычесть исходного объема из нового объема. И все, поздравляю!

Но если на вашем оригинальном контейнере нет весов:

4. Достаньте предмет.
5. Наполните вашу емкость водой до второй отметки, налейте этой воды в мерный цилиндр / другую мерную емкость.
6. Повторите шаг 6 для другого отмеченного уровня и вычтите объемы.
7. Пат себе на спину — вы нашли объем объекта неправильной формы!

Что измеряет объем?

Объем измеряет единиц пространства, занимаемого объектом в трех измерениях .Еще один близкий термин — вместимость, то есть объем внутреннего пространства объекта. Другими словами, вместимость описывает, сколько контейнер может вместить (воды, газа и т. Д.).

Каков объем Земли?

Объем Земли примерно равен 1,08321 × 10 ¹² км ³ ( 1,08 квадриллион кубических километров ), или 2,59876 × 10 ¹¹ кубических миль ( 259 триллионов кубических миль ). Вы можете получить этот результат, используя формулу объема сферы (4/3) ⨉ π ⨉ radius ³ и предполагая, что средний радиус Земли составляет 6371 километр (3958.76 миль).

Как рассчитать отношение площади поверхности к объему?

Чтобы вычислить отношение площади поверхности к объему SA: V, просто разделите площадь поверхности на объем . Для некоторых выбранных форм:

• Соотношение SA: V для куба = (сторона 6 ⨉ ² ) / (сторона ³ ) = 6 / сторона
• Отношение SA: V для сферы = (4 ⨉ π ⨉ радиус ² ) / ((4/3) ⨉ π ⨉ радиус ³ ) = 3 / радиус
• Соотношение SA: V для цилиндра = (2 ⨉ π ⨉ радиус ² + 2 ⨉ π ⨉ радиус ⨉ высота) / (π ⨉ радиус ² ⨉ высота) = 2 ⨉ (радиус + высота) / ( радиус ⨉ высота)

Как рассчитать объем

Расчет объема

Объем измеряется в кубах (или кубических единицах).

Сколько кубиков в этой прямоугольной призме (кубоиде)?

Мы можем считать кубики, хотя быстрее вычислить длину, ширину и высоту и использовать умножение. Прямоугольная призма выше имеет объем 48 кубических единиц.

Объем прямоугольной призмы = длина x ширина x высота

Примеры расчета площади прямоугольника

Нам нужно сделать два умножения, чтобы вычислить объем. Мы вычисляем площадь одной грани (или стороны) и умножаем ее на ее высоту.Примеры ниже показывают, как это можно сделать тремя способами.

Обратите внимание, как мы получаем один и тот же ответ независимо от того, какой стороной мы ищем область.

Когда ваш ребенок начинает работать с площадью и периметром, он или она обычно будет работать с двумя измерениями — квадратами, прямоугольниками, треугольниками и т. Д., Которые показаны на бумаге как плоские — нет глубины или третьего измерения. Работа с объемом действительно включает 3 измерения. Убедитесь, что ваш ребенок знает об этом и не думает о кубах и других трехмерных фигурах, показанных на бумаге, как о еще одной «фигуре на странице».«Покажите им настоящие коробки и покажите, как их можно нарисовать (или изобразить) на двухмерном листе бумаги. Другими словами, убедитесь, что существует связь между тем, что на бумаге, и тем, что она представляет в реальном мире.

Убедитесь, что вашего ребенка не смущает использование громкости , когда речь идет о громкости.

Единицы измерения объема

Есть очень большие различия между единицами измерения объема. Например, в 1 метре 100 сантиметров, а в кубическом метре 1 000 000 (да, 1 миллион) кубических сантиметров.

Почему большая разница? Потому что по объему у нас есть не только длина; у нас есть длина, ширина и высота. Пример кубика сахара ниже показывает это.

Сколько сахара? 1 м ³ или 1000000 см ³

Подумайте о заполнении очень большой коробки (шириной 1 метр, длиной 1 метр и высотой 1 метр) кубиками сахара (с каждой стороной 1 сантиметр).

	Шаг 1: один ряд вдоль дна коробки — , что составляет 100 кубиков сахара
	Шаг 2: накройте остальную часть основания коробки — , что даст в общей сложности 100 рядов с 100 кубиками сахара в каждом.100 x 100 = 10000 сахара кубиков на дне большой коробки.
	Шаг 3: Повторите это 99 раз, пока не получите слоев по 10 000 кубов, уложенных стопкой в ​​100 слоев. 10 000 x 100 = 1 000 000 кубиков сахара

1000000 см ³ в 1 м ³ — будьте осторожны, чтобы не было слишком много сахара!

Есть и другие единицы измерения объема; кубические дюймы, кубические футы, кубические ярды — все это единицы измерения объема.Миллилитры, литры, галлоны также используются, особенно при измерении жидкостей.

Не забывайте крошечный 3

Пишем кубические размеры с помощью маленькой 3 рядом с единицей. Пишем мм 3 , см 3 , м 3 , км 3 , см 3 Можно сказать «85 сантиметров в кубе» или «85 кубических сантиметров»

Примеры расчета объема прямоугольных призм

	Объем = длина x ширина x высота Объем = 12 см x 8 см x 6 см = 576 см 3
	Объем = длина x ширина x высота Объем = 20 м x 2 м x 2 м = 80 м 3
	Объем = длина x ширина x высота Объем = 10 м x 4 м x 5 м = 200 м 3

Объем цилиндра

Для вычисления объема цилиндра нужно умножить площадь основания на высоту цилиндра.Основание цилиндра круглое, а формула для вычисления площади круга: площадь круга = πr ² . Здесь больше о площади круга.

Объем = Площадь основания x Высота Объем = πr 2 x h Объем = πr 2 h

Примечание: в приведенных ниже примерах мы будем использовать 3,14 в качестве приблизительного значения для π (Pi).

Пример расчета объема цилиндра

Размеры указаны в см.

Объем = πr 2 ч Объем = 3,14 x 3 x 3 x 8 Объем = 226,08 см 3

Объем конуса

Объем конуса равен одной трети объема цилиндра с соответствующей высотой и площадью основания. Это дает формулу для объема конуса, как показано ниже.

Объем = 1/3 πr 2 ч

Пример расчета объема конуса

Размеры указаны в см.

Объем = 1/3 πr 2 ч Объем = 1/3 x 3,14 x 2 x 2 x 7 Объем = 29,31 см 3

Объем сферы

Формула объема шара приведена ниже.

Объем = 4/3 πr 3

Пример расчета объема сферы

Размеры указаны в см.

Объем = 4/3 πr 3 Объем = 4/3 x 3,14 x 4 x 4 x 4 Объем = 267,95 см 3

Рабочие листы для печати

Используйте таблицу ниже, чтобы попрактиковаться в вычислении объемов.

Здесь вы получите другие рабочие листы геометрии по периметру, площади и т. Д.

Калькулятор длины, ширины и высоты к объему

Нажмите «Сохранить настройки», чтобы перезагрузить страницу с уникальным адресом веб-страницы для создания закладок и обмена текущими настройками инструмента.

✕ очистить настройки

Инструмент «Отразить» с текущими настройками и рассчитать длину, ширину или высоту

К сожалению, здесь не удалось отобразить графику, потому что ваш браузер не поддерживает холст HTML5.

Сопутствующие инструменты

Руководство пользователя

Этот онлайн-инструмент вычисляет объем прямоугольной коробки, сплошного тела или пространства на основе размеров длины, ширины и высоты. Нет необходимости вводить значения в одних и тех же единицах измерения, просто выберите желаемые единицы для каждого измерения и рассчитанного объема.

После ввода размеров длины, ширины и высоты рассчитанный объем отобразится в поле ответа. Также будет показано изображение масштабированного трехмерного чертежа с правильными пропорциями и помечено каждым размером и рассчитанным объемом.

Формула

Формула, используемая данным калькулятором для расчета объема объекта прямоугольной формы:

В = Д · Ш · В

Символы

• V = Объем
• L = длина
• W = Ширина
• H = высота

Объемные размеры — длина, ширина и высота

Введите длину, ширину и высоту прямоугольной формы.

Для преобразования единиц измерения длины, ширины и высоты используются следующие коэффициенты преобразования единиц СИ в метры (м):

SI Метрические единицы длины префикса

• йоктометр (мкм) — 1 x 10 ^-24 м
• зептометр (zm) — 1 x 10 ^-21 м
• аттометр (am) — 1 x 10 ^-18 м
• фемтометр (фм) — 1 x 10 ^-15 м
• пикометр (пм) — 1 x 10 ^-12 м
• нанометр (нм) — 1 x 10 ^-9 м
• микрометр (мкм) — 0.000001 м
• миллиметр (мм) — 0,001 м
• сантиметр (см) — 0,01 м
• дециметр (дм) — 0,1 м
• метр (м) — 1 м
• декаметр (плотина) — 10 м
• гектометр (гм) — 100 м
• километр (км) — 1000 м
• мегаметр (мм) — 1000000 м
• гигаметр (Gm) — 1 x 10 ⁺⁹ м
• тераметр (Тм) — 1 x 10 ⁺¹² м
• петаметр (Pm) — 1 x 10 ⁺¹⁵ м
• exametre (Em) — 1 x 10 ⁺¹⁸ м
• зеттаметр (Zm) — 1 x 10 ⁺²¹ м
• йоттаметр (Ym) — 1 x 10 ⁺²⁴ м

Британские и американские единицы длины

• тысячная дюйма (тыс.) — 0.0000254 м
• дюйма (дюйм) — 0,0254 м
• фут — 0,3048 м
• ярд — 0,9144 м
• миля (миль) — 1609,344 м
• морская миля (морская миля) — 1852 м

Астрономических единиц

• астрономическая единица (а.е.) — 149 597 870 700 м
• световых года — 9,460,730,472,580,800 м
• парсек (шт) — 30 856 775 814 913 672,789… м
• килопарсек (кпк) — 3,08567758142789… x 10 ⁺¹⁹ м
• мегапарсек (Мпк) — 3.08567758142789… x 10 ⁺²² м
• гигапарсек (Гпк) — 3,08567758142789… x 10 ⁺²⁵ м

Расчет объема

Это объем прямоугольной формы, который соответствует размерам, указанным для длины, ширины и высоты. Объем рассчитывается путем умножения каждого измерения и последующего преобразования его в выбранные единицы измерения объема.

Для перевода расчетного объема в различные единицы измерения используются следующие коэффициенты пересчета в кубические метры (м³):

Метрические единицы измерения объема

• кубический нанометр (куб. Нм) — 1 x 10 ^-27 м³
• кубический микрометр (куб мкм) — 1 x 10 ^-18 м³
• кубический миллиметр (куб мм) — 1 x 10 ^-9 м³
• кубический сантиметр (куб см) — 1 x 10 ^-6 м³
• миллилитр (мл) — 1 x 10 ^-6 м³
• чайная ложка (ч.л., метрическая) — 5 x 10 ^-6 м³
• столовая ложка (столовая, метрическая) — 1.5 x 10 ^-5 м³
• стакан (метрический) — 2,5 x 10 ^-4 м³
• литр (л) — 1 x 10 ^-3 м³
• куб.м — 1 м³
• килолитр (kL) — 1 м³
• мегалитр (ML) — 1000 м³
• кубический километр (куб км) — 1 x 10 ⁺⁹ м³

Английские имперские единицы измерения объема

• тыс. Куб. (Тыс. Куб.) — 1,6387064 x 10 ^-14 м³
• кубический дюйм (у.е. дюйм) — 1,6387064 x 10 ^-5 м³
• жидкая унция (жидкая унция, английская система мер) — 2.84130625 x 10 ^-5 м³
• пинта (пинта, дюймовая) — 5,68 26125 x 10 ^-4 м³
• галлона (галлоны) — 4,54609 x 10 ^-3 м³
• кубических футов — 0,028316846592 м³
• кубический ярд (cu yd) — 0,764554857984 м³
• кубическая миля (cu mi) — 4168181825,440579584 м³
• кубическая морская миля (cu nmi) — 6352182208 м³

Единицы измерения объема в США

• тыс. Куб. (Тыс. Куб.) — 1,6387064 x 10 ^-14 м³
• чайная ложка (ч. Л., Сша) — 4.928375 x 10 ^-6 м³
• столовая ложка (Tbsp, usa) — 1.478676478125 x 10 ^-5 м³
• кубический дюйм (у.е. дюйм) — 1,6387064 x 10 ^-5 м³
• жидкая унция (жидкая унция, США) — 2,95735295625 x 10 ^-5 м³
• чашка (США) — 2.365882365 x 10 ^-4 м³
• пинта (pt, usa liquid) — 4,73176473 x 10 ^-4 м³
• галлона (галлон, жидкость США) — 3,785411784 x 10 ^-3 м³
• кубических футов — 0.028316846592 м³
• баррель (барр., Нефть) — 0,158987294928 м³
• кубический ярд (cu yd) — 0,764554857984 м³
• кубическая миля (cu mi) — 4168181825,440579584 м³
• кубическая морская миля (cu nmi) — 6352182208 м³

литров Метрическая префикс Единицы измерения объема

• йоктолитр (yL) — 1 x 10 ^-27 м³
• зептолитр (zL) — 1 x 10 ^-24 м³
• аттолитр (al) — 1 x 10 ^-21 м³
• фемтолитр (фл) — 1 x 10 ^-18 м³
• пиколитр (пл) — 1 x 10 ^-15 м³
• нанолитр (кв.нл) — 1 x 10 ^-12 м³
• микролитр (кв мкл) — 1 x 10 ^-9 м³
• миллилитр (кв. Мл) — 0.000001 м³
• сантилитр (кв.кл) — 0,00001 м³
• децилитр (дл) — 0,0001 м³
• литр (кв. Л) — 0,001 м²
• декалитр (дал) — 0,01 м³
• гектолитр (гл) — 0,1 м³
• килолитр (кв.кл) — 1 м³
• мегалитр (ML) — 1000 м³
• гигалитр (GL) — 1000000 м³
• тералитр (TL) — 1 x 10 ⁺⁹ м³
• петалитр (PL) — 1 x 10 ⁺¹² м³
• exalitre (EL) — 1 x 10 ⁺¹⁵ м³
• цетталитр (ZL) — 1 x 10 ⁺¹⁸ м³
• йотталитр (YL) — 1 x 10 ⁺²¹ м³

Кубические метры СИ Метрическая префикс Единицы измерения объема

• кубический йоктометр (куб.м) — 1 x 10 ^-72 м³
• кубический зептометр (куб. М3) — 1 x 10 ^-63 м³
• кубический аттометр (куб. М) — 1 x 10 ^-54 м³
• кубический фемтометр (куб фм) — 1 x 10 ^-45 м³
• кубический пикометр (куб.м.) — 1 x 10 ^-36 м³
• кубический нанометр (куб.нм) — 1 x 10 ^-27 м³
• кубический микрометр (куб мкм) — 1 x 10 ^-18 м³
• кубический миллиметр (куб мм) — 1 x 10 ^-9 м³
• кубический сантиметр (куб см) — 0.000001 м³
• кубический дециметр (куб дм) — 0,001 м³
• куб.м — 1 м³
• куб. Декаметр (куб. Дамба) — 1000 м³
• кубический гектометр (куб.м.) — 1000000 м³
• кубический километр (куб км) — 1 x 10 ⁺⁹ м³
• кубических мегамметров (куб. Мм) — 1 x 10 ⁺¹⁸ м³
• кубический гигаметр (куб.Гм) — 1 x 10 ⁺²⁷ м³
• кубический тераметр (куб.тм) — 1 x 10 ⁺³⁶ м³
• кубических петаметр (куб.м.) — 1 x 10 ⁺⁴⁵ м³
• кубический метр (куб.м.) — 1 x 10 ⁺⁵⁴ м³
• кубический зеттаметр (куб. М3) — 1 x 10 ⁺⁶³ м³
• кубический йоттаметр (куб.см) — 1 x 10 ⁺⁷² м³

Кубические астрономические единицы

• кубическая астрономическая единица (у.е.) — 3.347

  5810748964239359243 x 10 ⁺³³ м³

• кубический световой год (кубический световой год) — 8.4678666462371516595551248694562 x 10 ⁺⁴⁷ м³
• куб. Парсек (у.е. шт) — 2,937998946096347255544756436543… x 10 ⁺⁴⁹ м³
• кубических килопарсек (у.е. кпк) — 2,937998946096347255544756436543… x 10 ⁺⁵⁸ м³
• кубических мегапарсек (у.е. МПк) — 2,937998946096347255544756436543… x 10 ⁺⁶⁷ м³
• кубический гигапарсек (куб Гпк) — 2,937998946096347255544756436543… x 10 ⁺⁷⁶ м³

Приложения

Используйте этот калькулятор длины x ширины x высоты для определения объема в следующих приложениях:

• Объем отправляемой посылки для добавления в отгрузочные документы
• Объем гравия, необходимый для заполнения дорожки, парковки или проезжей части.
• Прямоугольный резервуар для хранения.
• Вместимость грузового отсека легкового, грузового автомобиля или фургона.
• Объем загрузки автомобиля для перемещения хранилища.
• Максимальный объем резервуара для воды.
• Сколько топлива необходимо для заправки бака.
• Размер связки, необходимый для предотвращения утечек и разливов из контейнеров IBC.
• Количество мешков, необходимых для каждого материала для строительного проекта.
• Количество почвы, необходимое для заполнения ящика сеялки.
• Количество воды, необходимое для заполнения аквариума / аквариума.
• Наполнитель для пруда.
• Вместимость складского помещения из габаритов.
• IBC вместимость.
• Объем плавательного бассейна.
• Возможное место для багажа внутри чемодана.
• Цементная смесь, необходимая для заполнения фундаментов / опор.
• Объем кузова пикапа.
• Объем корпуса аудиодинамика.
• Кормушка для кормления животных.
• Садовый сарай, солярий или парник, объем цементной подушки.

Справка

Резервуар 25 x 10 x 12 дюймов в галлонах США

Сколько галлонов США вмещает резервуар шириной 10 дюймов, высотой 12 дюймов и длиной 25 дюймов?

Если исходить из внутренних размеров или без толщины стенок, объем резервуара составляет 12,987013 галлонов США.

Расчетный объем | SkillsYouNeed

На этой странице объясняется, как рассчитать объем твердых объектов, т.е.е. насколько вы могли бы поместиться в предмет, если бы, например, вы залили его жидкостью.

Площадь — это мера того, сколько места находится внутри двухмерного объекта (подробнее см. Нашу страницу: Расчет площади).

Объем — это мера пространства внутри трехмерного объекта. Наша страница, посвященная трехмерным формам, объясняет основы таких форм.

В реальном мире вычисление объема, вероятно, не то, что вы будете использовать так часто, как вычисление площади.

Однако это все еще может быть важным. Возможность рассчитать объем позволит вам, например, определить, сколько у вас есть места для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете уместить в банку.

Это также может быть полезно для понимания того, что имеют в виду средства массовой информации, когда говорят о пропускной способности плотины или течении реки.

---

Примечание к агрегатам

---

Площадь выражается в квадратных единицах, потому что это два измерения, умноженные вместе.

Объем выражается в кубических единицах, потому что это сумма трех измерений (длина, ширина и глубина), умноженных вместе. Кубические единицы включают см ³ , м ³ и кубические футы.

ВНИМАНИЕ!

Объем также можно выразить как вместимость по жидкости.

Метрическая система

В метрической системе объем жидкости измеряется в литрах, что напрямую сопоставимо с кубическим размером, поскольку 1 мл = 1 см ³ .1 литр = 1000 мл = 1000 см ³ .

Британская / Английская система

В британской / британской системе эквивалентными измерениями являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше придерживаться жидких или твердых единиц объема.

Дополнительную информацию см. На нашей странице Системы измерения

---

Основные формулы для расчета объема

Объем твердых тел на основе прямоугольников

В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.

То, как вы относитесь к различным размерам, не меняет расчет: например, вы можете использовать «глубину» вместо «высоты». Важно то, что все три измерения умножаются. Вы можете умножать в любом порядке, поскольку это не изменит ответ (подробнее см. Нашу страницу, посвященную умножению на ).

Коробка размером 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см ³

---

Объем призм и цилиндров

Эту базовую формулу можно расширить, чтобы охватить объем цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.

Фактически, для цилиндров и призм объем — это площадь одной стороны, умноженная на глубину или высоту формы.

Таким образом, основная формула для определения объема призм и цилиндров:

Площадь формы торца × высота / глубина призмы / цилиндра.

---

Объем конусов и пирамид

Тот же принцип, что и выше (ширина × длина × высота), применяется для вычисления объема конуса или пирамиды, за исключением того, что, поскольку они достигают точки, объем составляет только долю от общего количества, которое было бы, если бы они продолжались. в той же форме насквозь.

Объем конуса или пирамиды составляет ровно одну треть от объема коробки или цилиндра с таким же основанием.

Таким образом, формула:

Площадь формы основания или конца × высота конуса / пирамиды × ¹ / ₃

Вернитесь на нашу страницу Расчет площади , если вы не можете вспомнить, как рассчитать площадь круга или треугольника.

Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:

Площадь внутри круга = πr2 (где π (pi) приблизительно равно 3.14 и r — радиус окружности).

В этом примере площадь основания (круга) = πr ² = 3,14
× 5 × 5 = 78,5 см ² .

78,5 × 10 = 785

785 × 1/3 = 261,6667 см ³

---

Объем сферы

Как и в случае с кругом, вам нужно π (пи) для вычисления объема сферы.

Формула: 4/3 × π × радиус ³ .

Вам может быть интересно, как определить радиус шара.Если не протыкать через него спицу (эффективный, но конечный для мяча!), Есть способ попроще.

Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.

Длина окружности рассчитывается как 2 x π x радиус.

Чтобы вычислить радиус из окружности, вы:

Разделите окружность на (2 x π) .

---

Рабочие примеры: расчет объема

Пример 1

Вычислите объем цилиндра длиной 20 см, круговой конец которого имеет радиус 2,5 см.

Сначала проработайте площадь одного из круглых концов цилиндра.

Площадь круга равна πr ² (π × радиус × радиус). π (пи) приблизительно равно 3,14.

Таким образом, площадь конца равна:

3.14 x 2,5 x 2,5 = 19,63 см ²

Объем — это площадь конца, умноженная на длину, и, следовательно, составляет:

19,63 см ² x 20 см = 392,70 см ³

Пример 2

Что больше по объему: сфера радиусом 2 см или пирамида с основанием в квадрате 2,5 см и высотой 10 см?

Сначала определим объем сферы .

Объем сферы равен 4/3 × π × радиус ³ .

Таким образом, объем сферы составляет:

.

4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см ³

Затем определите объем пирамиды .

Объем пирамиды 1/3 × площадь основания × высота.

Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см ²

Объем, следовательно, равен 1/3 x 6,25 × 10 = 20.83 см ³

Таким образом, сфера больше по объему, чем пирамида.

---

Расчет объема твердых частиц неправильной формы

Точно так же, как вы можете вычислить площадь неправильных двумерных форм, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных твердых тел. Просто разделите твердое тело на более мелкие части, пока не получите только твердые тела, с которыми вы сможете легко работать.

Рабочий пример

Вычислите объем водяного цилиндра общей высотой 1 м, диаметром 40 см и полусферической верхней частью.

Сначала вы делите фигуру на две части: цилиндр и полусферу (полусферу).

Объем сферы равен 4/3 × π × радиус ³ . В этом примере радиус составляет 20 см (половина диаметра). Поскольку верхняя часть является полусферической, ее объем будет вдвое меньше полной сферы. Таким образом, объем данного участка формы:

.

0,5 × 4/3 × π × 203 = 16,755,16 см ³

Объем цилиндра равен площади основания × высоте.Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, которая составляет 1 м — 20 см = 80 см. Площадь цоколя ² грн.

Таким образом, объем цилиндрического сечения данной формы составляет:

80 × π × 20 × 20 = 100 530,96 см ³

Таким образом, общий объем этого резервуара для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см ³ .

Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000 см ³ ). Однако вполне правильно выразить его как cm ³ , поскольку задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.

---

Дополнительная литература по навыкам, которые вам нужны

---

Понимание геометрии
Часть необходимых навыков Руководство по счету

Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел.